Importar parámetros de MS Excel

Librería

Para empezar, la guía se realizará en base al problema de Family Knapsack que se introdujo como ejemplo en la guía Matemáticas en MS Office. El primer paso es importar la libreria openpyxl con la siguiente línea de código:

from openpyxl import*

Nota

De forma que la línea de código funcione en cualquier computador sin tener que actualizarla, se recomienda guardar el archivo con los parámetros en la misma carpeta en la que se encuentra el archivo de la implementación del problema. Para lograr esto, la ruta se escribe con un punto seguido de un slash ./ y el nombre del archivo con los parámetros. El punto hace automaticamente la referencia a la misma carpeta donde se encuentra el archivo en el que se esta realizando la implementación.

Libro de MS Excel y hojas

Luego, es necesario importar el libro de MS Excel donde se encuentran los parámetros del problema de optimización a resolver. En este caso, el libro de parámetros se llama parametros.xlsx. El archivo se importa con la función load_wokbook() que recibe como parámetro la ruta donde se encuentra el archivo. Además, para poder realizar operaciones con el libro más adelante, se guardará el archivo en una nueva variable que se llamará book.

book = load_workbook("./parametros.xlsx")

Ahora, se debe guardar cada una de las hojas que tiene el libro de Excel. En el ejemplo que estamos usando, el libro con los parámetros tiene tres hojas.

A continuación se ilustra como guardar cada hoja.

Nota

En caso de que solo exista una hoja se puede utilizar únicamente la siguiente línea de código:

sheet = book.active

sheet1 = book["pesoObjetos"]
sheet2 = book["pesoMaxExcursionistas"]
sheet3 = book["preferencias"]

Parámetros

Nota

El número de recorridos depende del número de conjuntos en los que esta indexado el parámetro en cuestión. En caso de que este indexado en tres o más conjuntos, se deberan construir varias tablas con ciertos índices fijos y se tendrán máximo dos recorridos (filas y columnas).

Nota

Cada recorrido se definirá según dónde se encuentre la información en el archivo de excel.

Con lo anterior, se procede a guardar los parámetros en diccionarios. Para cada parámetro se debe seguir el siguiente procedimiento:

1. Crear el diccionario donde se guardará su información.

2. Realizar uno o dos recorridos para pasar por los valores de cada uno de los índices del parámetro.

3. Dentro del recorrido se guarda cada índice del parámetro en una variable.

4. Dentro del recorrido se guarda el valor del índice en el diccionario donde los índices seran las llaves.

En la primera hoja se encuentra el parámetro \(p_i\) que hace referencia al peso de cada uno de los objetos.

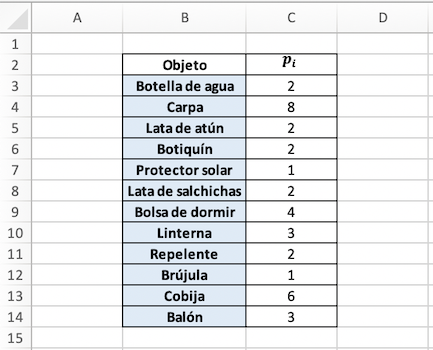
Como este parámetro esta indexado únicamente en el conjunto de objetos, solo se debe realizar un recorrido. Este recorrido se definirá entre 3 y 14, pues estas son las filas donde se encuentran los valores de este parámetro para cada uno de los objetos. Para extraer el valor de una celda de Excel se utilizará el comando .value.

Nota

Es importante recordar que la función range(i,j) define una serie de números desde i hasta j-1. Es por esto que, en este caso, se utiliza el número 15 como j.

Nota

Es importante recordar que en la función cell(i,j), i hace referencia a la fila y j a la columna. En este caso, como los índices (nombre de cada objeto) se encuentran en la segunda columna, se utiliza el número 2 como j para todas las iteraciones.

# 1. Se crea el diccionario para guardar la información del parámetro
p = {}  #Peso de los objetos

# 2. Se realiza el recorrido para guardar todos los valores necesarios
for i in range(3,15):
    objeto = sheet1.cell(i,2).value       # 3. Se guarda cada índice para luego utilizarlo como llave en el diccionario
    p[objeto] = sheet1.cell(i,3).value    # 4. Se guarda el valor del índice correspondiente a la iteración

# Se imprime el diccionario para verificar que se hayan importado correctamente los datos
print(p)

{'Botella de agua': 2, 'Carpa': 8, 'Lata de atún': 2, 'Botiquín': 2, 'Protector solar': 1, 'Lata de salchichas': 2, 'Bolsa de dormir': 4, 'Linterna': 3, 'Repelente': 2, 'Brújula': 1, 'Cobija': 6, 'Balón': 3}

Los siguientes parámetros se encuentra en la segunda y tercera hoja. En la segunda hoja está el parámetro \(b_j\) que hace referencia al peso máximo que puede cargar cada excursionista.

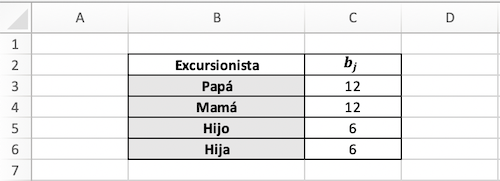
En la tercera hoja está el parámetro \(q_{ij}\) que hace referencia a la preferencia que tiene cada excursionista sobre cada objeto.

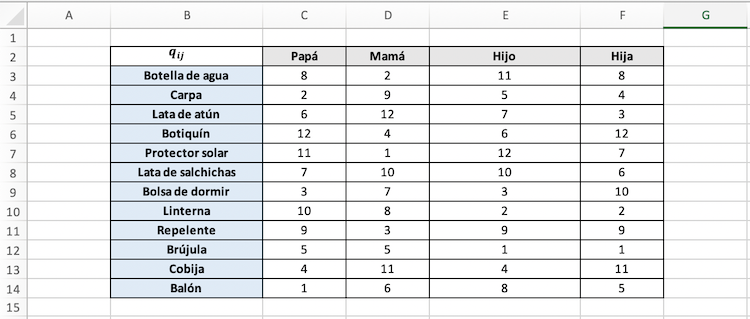
Para cargar estos parámetro se realiza lo mismo que para \(p_i\) teniendo en cuenta el cambio de rango donde esta la información. Además, como \(q_{ij}\) esta indexado en dos conjuntos, se deben realizar dos recorridos y las llaves del diccionario serán tuplas.

b = {} #Peso máximo por excursionista

for i in range(3,7):
    excursionista = sheet2.cell(i,2).value       
    b[excursionista] = sheet2.cell(i,3).value    

print("b:")
print(b)


q = {} #Preferencia por cada excursionista de cada objeto

for i in range(3,15):
    for j in range(3,7):
        objeto = sheet3.cell(i,2).value
        excursionista = sheet3.cell(2,j).value
        q[(objeto,excursionista)]=sheet3.cell(i,j).value

print()
print("q:")
print(q)

b:
{'Papá': 12, 'Mamá': 12, 'Hijo': 6, 'Hija': 6}

q:
{('Botella de agua', 'Papá'): 8, ('Botella de agua', 'Mamá'): 2, ('Botella de agua', 'Hijo'): 11, ('Botella de agua', 'Hija'): 8, ('Carpa', 'Papá'): 2, ('Carpa', 'Mamá'): 9, ('Carpa', 'Hijo'): 5, ('Carpa', 'Hija'): 4, ('Lata de atún', 'Papá'): 6, ('Lata de atún', 'Mamá'): 12, ('Lata de atún', 'Hijo'): 7, ('Lata de atún', 'Hija'): 3, ('Botiquín', 'Papá'): 12, ('Botiquín', 'Mamá'): 4, ('Botiquín', 'Hijo'): 6, ('Botiquín', 'Hija'): 12, ('Protector solar', 'Papá'): 11, ('Protector solar', 'Mamá'): 1, ('Protector solar', 'Hijo'): 12, ('Protector solar', 'Hija'): 7, ('Lata de salchichas', 'Papá'): 7, ('Lata de salchichas', 'Mamá'): 10, ('Lata de salchichas', 'Hijo'): 10, ('Lata de salchichas', 'Hija'): 6, ('Bolsa de dormir', 'Papá'): 3, ('Bolsa de dormir', 'Mamá'): 7, ('Bolsa de dormir', 'Hijo'): 3, ('Bolsa de dormir', 'Hija'): 10, ('Linterna', 'Papá'): 10, ('Linterna', 'Mamá'): 8, ('Linterna', 'Hijo'): 2, ('Linterna', 'Hija'): 2, ('Repelente', 'Papá'): 9, ('Repelente', 'Mamá'): 3, ('Repelente', 'Hijo'): 9, ('Repelente', 'Hija'): 9, ('Brújula', 'Papá'): 5, ('Brújula', 'Mamá'): 5, ('Brújula', 'Hijo'): 1, ('Brújula', 'Hija'): 1, ('Cobija', 'Papá'): 4, ('Cobija', 'Mamá'): 11, ('Cobija', 'Hijo'): 4, ('Cobija', 'Hija'): 11, ('Balón', 'Papá'): 1, ('Balón', 'Mamá'): 6, ('Balón', 'Hijo'): 8, ('Balón', 'Hija'): 5}

Conjuntos

Finalmente, se construyen los conjuntos a partir de las llaves de los diccionarios que ya se crearon para los parámetros. Como el parametro \(p_i\) esta indexado en el conjunto de objetos, éste tiene como llaves a todos los objetos. Por lo tanto, el conjunto de objetos, que se declarará como una lista, se construye con la siguiente línea de código:

O = list(p.keys())

# Se imprime la lista para verificar que se haya construido correctamente el conjunto
print(O)

['Botella de agua', 'Carpa', 'Lata de atún', 'Botiquín', 'Protector solar', 'Lata de salchichas', 'Bolsa de dormir', 'Linterna', 'Repelente', 'Brújula', 'Cobija', 'Balón']

Lo mismo se realiza para construir el conjunto de excursionistas, pero en este caso a partir del parametro \(b_j\) ya que éste esta indexado en el conjunto deseado.

E = list(b.keys())

# Se imprime la lista para verificar que se haya construido correctamente el conjunto
print(E)

['Papá', 'Mamá', 'Hijo', 'Hija']

Siguiente paso

Con los parámetros importados y los conjuntos construidos se puede proceder a la implementación y solución del problema de optimización.

Créditos

Equipo de Optimización
Desarrollo: Daniel Yamin, Juan F. Rengifo
Fecha: 25/11/2020