Búsqueda Local

Tags: Búsqueda Local, Heurística, Variable Continua

Show code cell source Hide code cell source

import os
# Por precaución, cambiamos el directorio activo de Python a aquel que contenga este notebook
if "optimizacion" in os.listdir():
    os.chdir(r"optimizacion/Formulaciones/9. Busqueda local/")

Prerrequisitos:

• Ver video búsqueda local

• Ver video introducción a Python: funciones

• Ver video introducción a Python: estructuras de control

Objetivos:

Implementar un algorítmo de búsqueda local.

Implementación búsqueda local

En el script busquedaLocal.py hay una implementación para un algoritmo de búsqueda local. Esta implementación consiste principalmente de una función (busquedaLocal) que realiza la búsqueda local para un problema que le entra por parámetro. Además de esto, a la función también le debemos pasar por parámetro el radar con el que vamos a hacer la búsqueda local, y el punto inicial de la búsqueda. A continuación vamos a ver como funciona esta implementación, y mas detalladamente que es cada uno de los argumentos que le debemos pasar a la función busquedaLocal para haga la búsqueda local correctamente. Lo primero que debemos hacer es importar el script:

import busquedaLocal as bl

Nota: Recuerde, puede usar la función help para consultar la documentación de cada una de las funciones del módulo (help(bl.busquedaLocal)).

La función busquedaLocal recibe cinco argumentos:

1. f : Una función de Python que retorna el valor de la función objetivo dado un punto \((x_1,x_2)\)

2. restricciones: Una lista de Python con las restricciones del modelo en un formato específico

3. radar: Una función de Python que dado un punto \((x_1,x_2)\) y un radio (d), retorna una lista con los puntos en el radar

4. x0: Una tupla de Python con el punto inicial de la búsqueda

5. d0: El radio del radar de búsqueda

Veamos entonces como construir cada argumento para el problema de la empresa 2Crudos inc. que hemos visto. Recordemos, la formulación del problema es la siguiente:

\[ \begin{equation}\label{eq:fo} \min \ 20x_1+15x_2 \end{equation} \]

Sujeto a,

\[\begin{split} \begin{align} 0.3x_1+0.4x_2&\ge 2000;\label{eq:c1}\\ 0.4x_1+0.2x_2&\ge 1500;\label{eq:c2}\\ 0.2x_1+0.3x_2&\ge 500;\label{eq:c3}\\ x_1 &\le 9000;\label{eq:c4}\\ x_2&\le 6000;\label{eq:c5}\\ x_1 &\ge 0;\label{eq:c6}\\ x_2&\ge 0.\label{eq:c7}\\ \end{align} \end{split}\]

1. Argumento f

El argumento f es una función de Python que retorna el valor de la función objetivo dado un punto \((x_1,x_2)\). Es decir, debemos declarar una función que dados unos puntos \((x_1,x_2)\), retorne \(20x_1+15x_2\). Esto lo hacemos de la siguiente forma:

# Función que retorna el valor de la función objetivo, para un punto (x1,x2)
def f(x1, x2):
    return 20 * x1 + 15 * x2

Veamos que hace la función que definimos:

x1, x2 = 6000, 3500
print(f"El valor de la función objetivo en el punto ({x1}, {x2}) es {f(x1, x2)}.")

El valor de la función objetivo en el punto (6000, 3500) es 172500.

2. Argumento restricciones

El argumento restricciones es una lista de Python con las restricciones del modelo. La forma en la que debemos pasar las restricciones del modelo es también como funciones, pero en este caso son funciones que retornan un valor booleano. Es decir retornan True si el punto \((x_1,x_2)\) cumple con la restricción, y retornan False de lo contrario. Veamos entonces como declarar estas funciones para cada una de las restricciones del modelo:

Consideremos entonces la siguiente restricción:

\[ \begin{equation*} 0.3x_1+0.4x_2\ge 2000; \end{equation*} \]

Para definir una función que, dado un punto \((x_1,x_2)\), retorna True si el punto cumple con la restricción, y False de lo contrario hacemos lo siguiente:

def R1(x1, x2):
    return 0.3 * x1 + 0.4 * x2 >= 2000

Veamos que hace la función que declaramos:

x1, x2 = 1000, 6000
print(f"R1({x1}, {x2}) retorna: {R1(x1, x2)}.")

R1(1000, 6000) retorna: True.

De la misma forma definimos una función booleana por cada restricción del modelo de la siguiente forma:

# Función booleana para la restricción (3)
def R2(x1, x2):
    return 0.4 * x1 + 0.2 * x2 >= 1500


# Función booleana para la restricción (4)
def R3(x1, x2):
    return 0.2 * x1 + 0.3 * x2 >= 500


# Función booleana para la restricción (5)
def R4(x1, x2):
    return x1 <= 9000


# Función booleana para la restricción (6)
def R5(x1, x2):
    return x2 <= 6000


# Función booleana para la restricción (7)
def R6(x1, x2):
    return x1 >= 0


# Función booleana para la restricción (8)
def R7(x1, x2):
    return x2 >= 0

Ahora, como el argumento restricciones es una lista de estas funciones, pues lo único que debemos hacer es almacenar todas estas funciones en una lista de Python. Esto lo hacemos de la siguiente forma:

restricciones = [R1, R2, R3, R4, R5, R6, R7]

3. Argumento radar

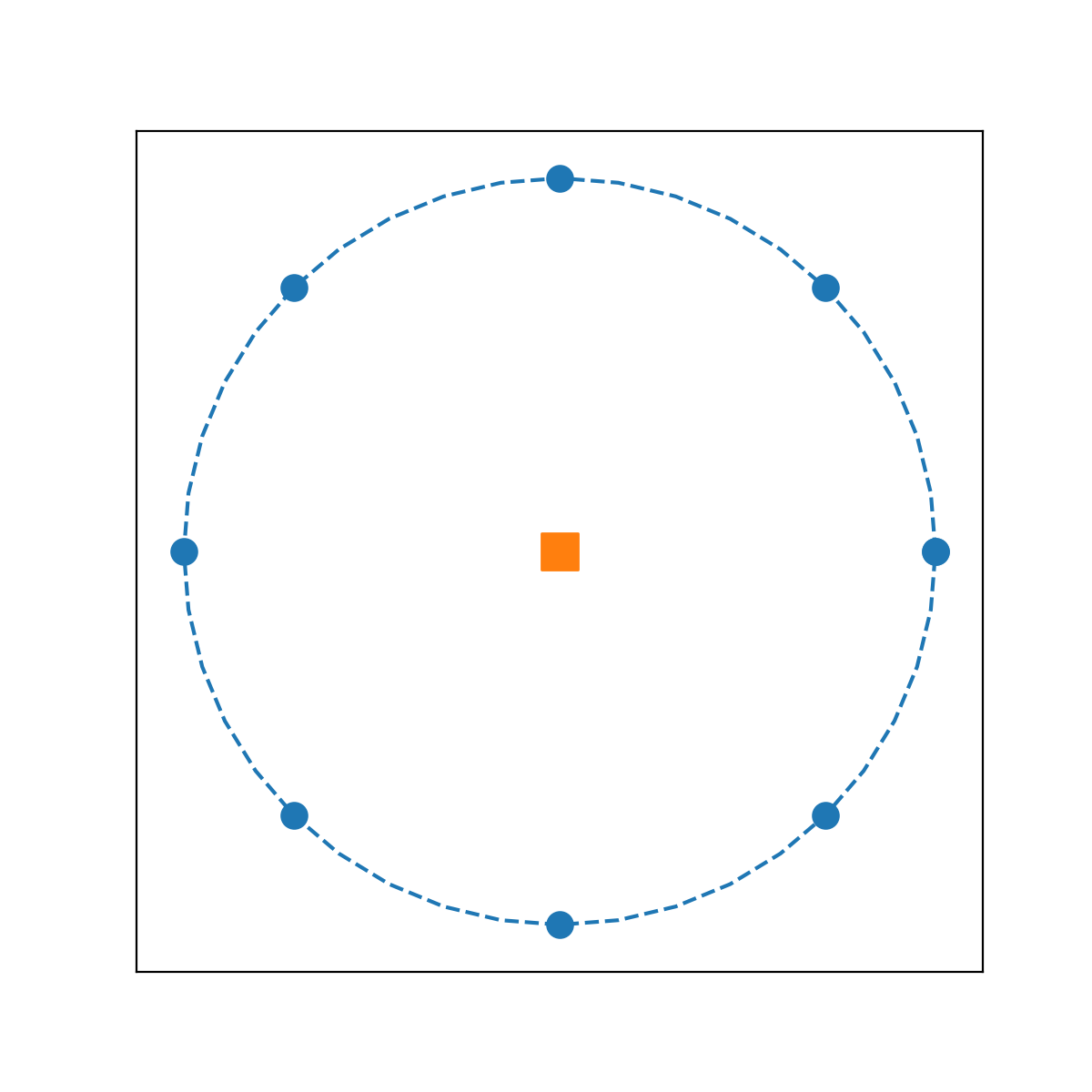
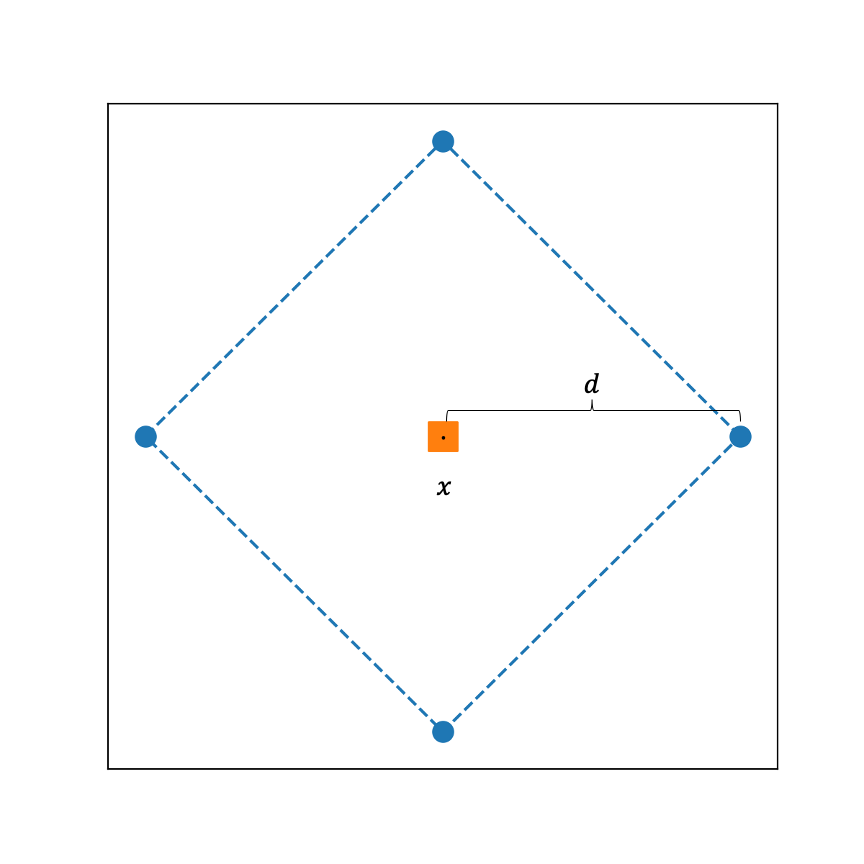
El argumento radar es una función de Python que dado un punto \((x_1,x_2)\) y un radio (d), retorna una lista con los puntos en el radar. En el script BusquedaLocal.py que importamos al principio del notebook hay una implementación de esta función. En la función miRadar(x,d) esta implementada para un radar circular de 8 puntos, como el que se muestra en la siguiente figura.

Veamos entonces la documentación de esta función:

help(bl.miRadar)

Help on function miRadar in module busquedaLocal:

miRadar(x, d, n=8)
    Se usa la ecuación paramétrica del circulo para crear un radar circular.
    Puede consultar el siguiente link para mas información sobre esta ecuación:
    http://jwilson.coe.uga.edu/EMAT6680Fa05/Schultz/Assignment10/Parametric_Circles#:~:text=In%20parametric%20equations%2C%20each%20variable,0%2C%202*pi%5D).&text=At%20t%3D0%2C%20x%20%3D,or%20(1%2C%200)
    
    ROUTINE:
            miRadar(x,d)
    PURPOSE:
            Crear los puntos en el radar de búsqueda.
    
    ARGUMENTS:
            x (tuple): Punto central del radar.
            d (float): Radio del radar de búsqueda.
    
    RETURN VALUE:
            Una lista con los puntos en el radar.
    
    EXAMPLE:
            puntosRadar = radar((0,0),1)

4. Argumento x0

El argumento x0 hace referencia al punto factible en el que se inicia la búsqueda. Este argumento es un tupla de Python. En este caso, tomemos como punto inicial \((9000,6000)\) que sabemos que es un punto factible.

x0 = (9000, 6000)

5. Argumento d

Finalmente, el argumento d, de tipo float, hace referencia al radio de búsqueda, es decir, la distancia a los puntos que evalúa la exploración en cada iteración. Para este ejemplo tomemos d=500.

d0 = 500

6. Llamar la función

Ya teniendo claros todos los argumentos de la función busquedaLocal, debemos únicamente llamarla, con los argumentos que acabamos de crear, para correr el procedimiento de búsqueda local para nuestro problema. En la siguiente celda de código se corre la función busquedaLocal que retorna el valor de las variables de decisión del mejor punto que encontró. Este valor lo guardamos en la variable xStar.

xStar = bl.busquedaLocal(f, restricciones, bl.miRadar, x0, d0)

Ahora para ver el valor de las variables de decisión a los que llega nuestro procedimiento, podemos usar la función print() de Python.

print(f"El valor de las variables de decisión es {xStar}.")

El valor de las variables de decisión es (1989.5923599143498, 3525.126265847085).

Para ver el costo que tiene esta solución, es decir el valor en la función objetivo, podemos usar la función f() que declaramos, pasándole como argumento las componentes de xStar.

x1Star, x2Star = xStar
print(f"El costo total de esta solución es de ${f(x1Star, x2Star)}.")

El costo total de esta solución es de $92668.74118599328.

Si quisiéramos verificar que el punto que obtuvimos cumple con todas nuestras restricciones, podemos usar también las funciones booleanas que declaramos para hacer esta verificación:

for i,r in enumerate(restricciones):
    print(f"La evaluación de R{i + 1} es: {r(x1Star, x2Star)}.")

La evaluación de R1 es: True.
La evaluación de R2 es: True.
La evaluación de R3 es: True.
La evaluación de R4 es: True.
La evaluación de R5 es: True.
La evaluación de R6 es: True.
La evaluación de R7 es: True.

Como podemos ver, nuestro punto xStar cumple con todas las restricciones.

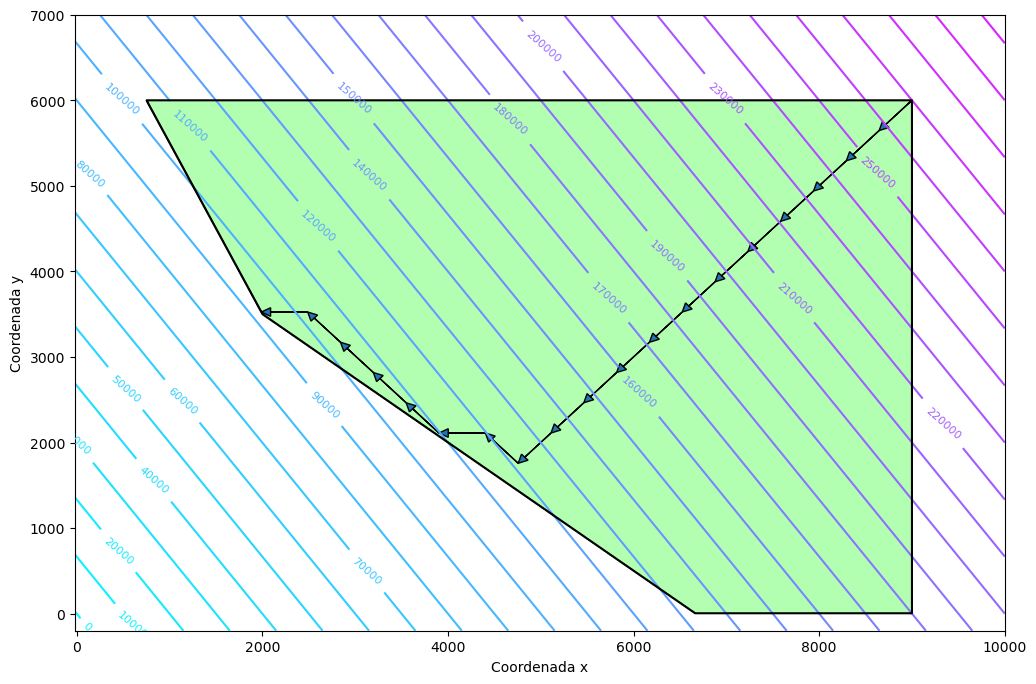
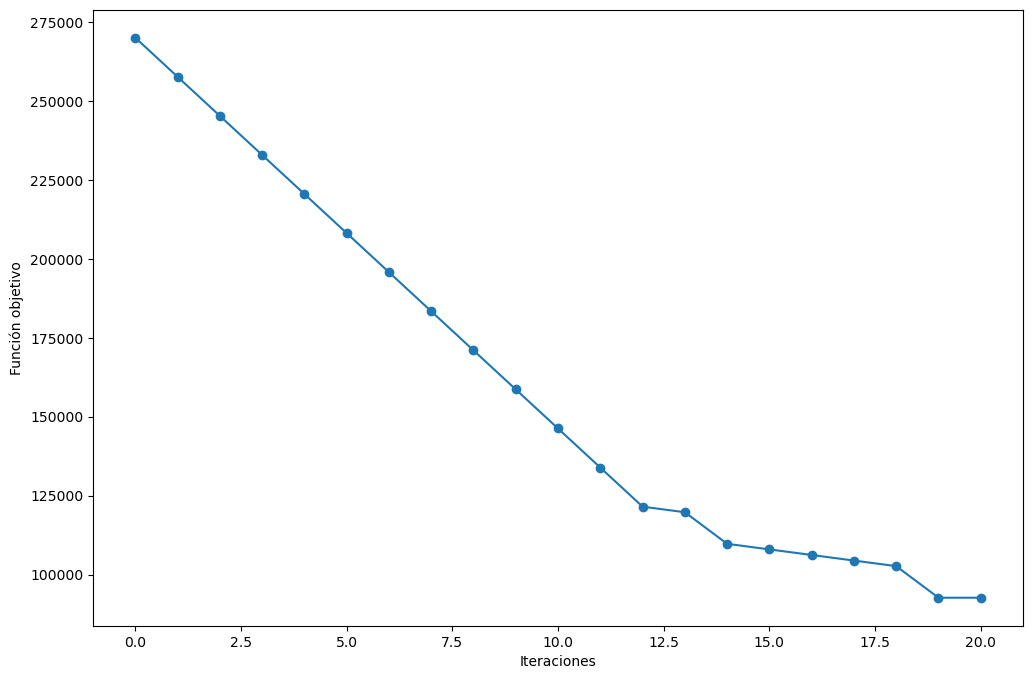
7. Representación gráfica del procedimiento

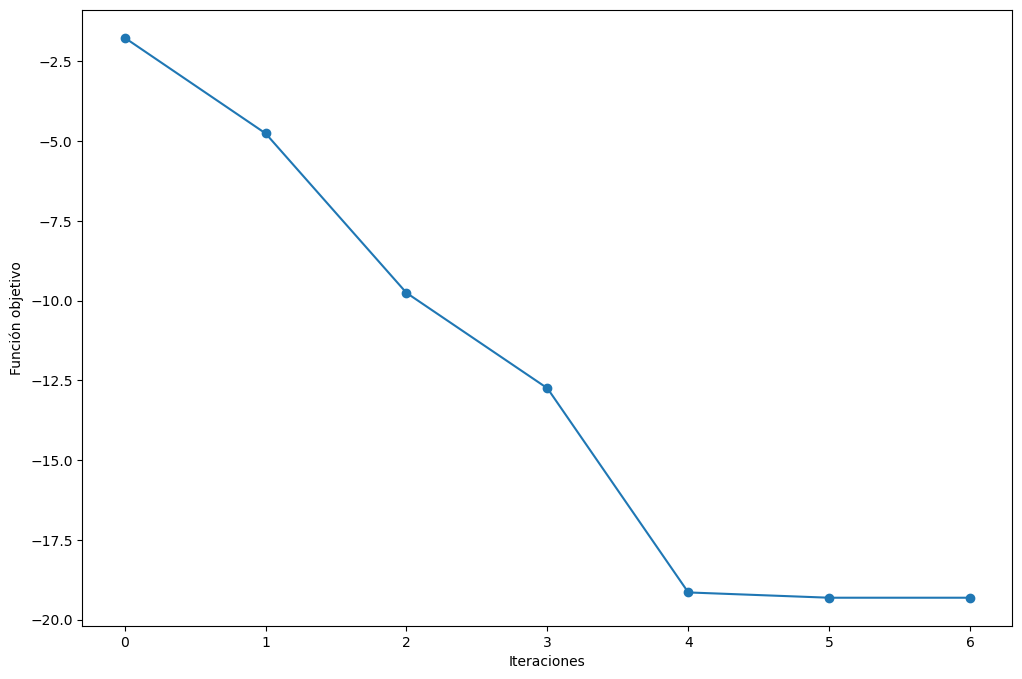
El script busquedaLocal.py que importamos al principio del notebook, también tiene una función que corre el procedimiento de búsqueda local, y además grafica lo que se hizo en cada iteración. Esta función se llama busquedaLocalGrafica y tiene lo mismos argumentos de busquedaLocal, mas el de xlim y ylim, estos últimos son argumentos para crear la gráfica únicamente, y representan los límites de la misma. Esta función genera dos gráficas: la primera gráfica muestra la región factible del problema, con las curvas de nivel (isóclinas) de la función objetivo, y la trayectoria que sigue el procedimiento de búsqueda local; la segunda gráfica muestra como se comporta el valor de la función objetivo contra las iteraciones del método.

bl.busquedaLocalGrafica(
    f, restricciones, bl.miRadar, x0, d0, xlim=[-20, 10000], ylim=[-200, 7000]
)

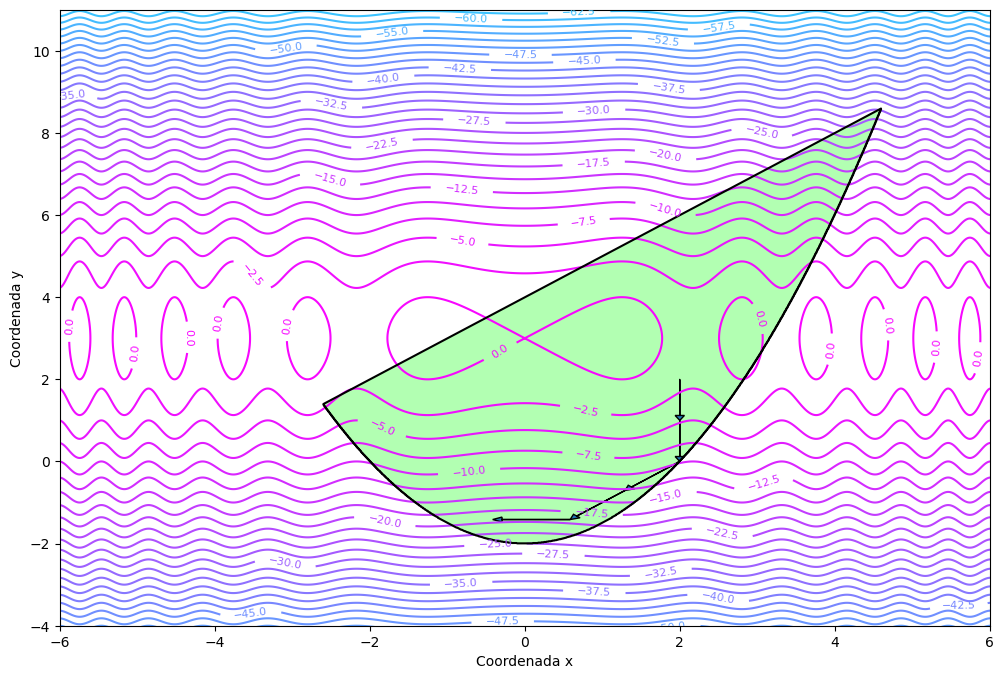
8. Modelo no lineal

Recuerde que con el método de búsqueda local podemos atacar problemas con restricciones y funciones objetivo no lineales. Consideremos entonces el siguiente modelo de optimización:

\[ \begin{equation*} \operatorname{mín}\ \sin{(x_1^2)}-(x_2-3)^2 \end{equation*} \]

Sujeto a,

\[\begin{split} \begin{align*} \frac{x_1^2}{2}-x_2&\le 2;\\ -x_1++x_2&\le 4. \end{align*} \end{split}\]

from numpy import cos, sin

# Se define la función Objetivo
def f(x1, x2):
    return sin(x1**2) - (x2 - 3) ** 2


# Se definen las restricciones
def R1(x1, x2):
    return (x1**2) / 2 - x2 <= 2


def R2(x1, x2):
    return -x1 + x2 <= 4


restricciones = [R1, R2]

# Se define un punto de partida y la distancia del radar
x0 = (2, 2)
d0 = 1

# Se ejecuta la búsqueda y se guarda el resultado
xStar = bl.busquedaLocal(f, restricciones, bl.miRadar, x0, d0)

# Se ilustra la búsqueda
print(f"El valor de la función objetivo es: {f(*xStar)}.")
bl.busquedaLocalGrafica(
    f, restricciones, bl.miRadar, x0, d0, xlim=[-6, 6], ylim=[-4, 11]
)

El valor de la función objetivo es: -19.314549033193508.

Ejercicio

Cree su propio radar de búsqueda, que reciba como paráetro un punto \(x \in \mathbb{R}^{2}\) y un radio \(d\) y genere los siguientes puntos:

En la siguiente celda de código implementa la función suRadar(x,d):

# Implemente su función de radar
def suRadar(x, d):
    """
    ROUTINE:
        SuRadar(x,d)
    PURPOSE:
        Crear los puntos en el radar de búsqueda.

    ARGUMENTS:
        x (tuple): Punto central del radar.
        d (float): Radio del radar de búsqueda.
    RETURN VALUE:
        Una lista con los puntos en el radar.
    EXAMPLE:
        puntosRadar = radar((0,0),1)
    """
    # Escribe a partir de esta linea tu código
    ...

Corre la función busquedaLocal con tu función suRadar y compara los resultados obtenidos con el radar miRadar.

Bono 1

Modifica la función suBusquedaLocal_dist() para que reduzca el radio del radar cuando no encuentre puntos mejores con el radio actual. Compara los resultados, ¿Mejora el valor de la función objetivo con este cambio?

Nota: Nota que en este caso deberá cambiar la condición de parada.

def suBusquedaLocal_dist():
    # Escribe a partir de esta linea tu código
    ...

#Usa esta celda de código para llamar tu modificción a la función.

Bono 2

Cree la función suBusquedaLocal_recur() con el mismo comportamiento de busquedaLocal() de forma que se propague en cada punto del radar recursivamente y halle el mejor punto de la región factible. Compare los resultados, ¿Mejora el valor de la función objetivo con este cambio?

Nota: Deberá cambiar la condición de parada de forma que no se repita la recursión indefinidamente.

def suBusquedaLocal_recur():
    # Escribe a partir de esta linea tu código
    ...

# Usa esta celda de código para llamar tu modificción a la función.

Créditos

Equipo Principios de Optimización
Autores: David Corredor y Jorge Huertas
Desarrollo: Alfaima Solano y Alejandro Mantilla
Última fecha de modificación: 08/04/2023