Producción de cemento - Solución

Producción de cemento - Solución#

Tags: Inventario

Enunciado#

Artos S.A. es una empresa dedicada a la producción de cemento que cuenta con una única planta en la ciudad de Barranquilla. La empresa debe determinar la cantidad de toneladas de cemento a producir en cada una de las siguientes 12 semanas. Los costos de producción, costos de almacenamiento, así como la demanda y el precio por tonelada de cemento, varían semana a semana y se presentan en la siguiente tabla.

Tabla 1. Estructura de costos y precio

Semana	Costo de producción [Miles de COP/ton]	Costo de almacenamiento [Miles de COP/ton]	Demanda [ton]	Precio [Miles de COP/ton]
1	172.8	6.9	95,000	432.0
2	178.7	7.2	99,750	440.6
3	174.6	8.0	104,738	449.5
4	181.4	8.9	109,974	458.4
5	183.0	9.0	109,974	467.6
6	177.7	7.8	109,974	477.0
7	182.8	6.7	120,972	486.5
8	186.8	7.3	120,972	496.2
9	181.8	7.8	108,875	506.2
10	178.3	8.8	97,987	516.3
11	173.4	9.2	78,390	526.6
12	168.8	8.4	94,068	537.1

Tenga en cuenta que, al inicio de la planeación, se cuenta con 12,000 toneladas de cemento y que, por especificaciones de la maquinaria, no se puede producir más de 110,000 toneladas ni menos de 85,000 toneladas en una semana cualquiera. El objetivo de Artos S.A. es maximizar su utilidad.

Formulación#

a. Formula matemáticamente un modelo de optimización de forma general que represente la situación anterior. Defina clara y rigurosamente:

Conjuntos
Parámetros
Variables de decisión
Restricciones
Naturaleza de las variables
Función objetivo

Conjuntos#

\(S\): Conjunto de semanas

Parámetros#

\(d_{i}\): demanda de la semana \(i\in S\)
\(p_{i}\): precio por tonelada de cemento en la semana \(i\in S\)
\(c_i\): costo de producir una tonelada de cemento en la semana \(i\in S\)
\(h_i\): costo de almacenamiento de una tonelada de cemento en la semana \(i\in S\)
\(I_0\): inventario inicial de toneladas de cemento

Variables de decisión#

\(x_{i}\): toneladas de cemento a producir en la semana \(i\in S\)
\(I_i\): toneladas de cemento que se tienen en inventario al final de la semana \(i\in S\)

Restricciones#

Se deben respetar los límites de producción:

\[\begin{split} \begin{align*} x_i&\leq 110000, &&\forall i \in S;\\ x_i&\geq 85000, &&\forall i \in S;\\ \end{align*} \end{split}\]

Restricción que contabiliza el inventario de cada semana:

\[\begin{split} \begin{align*} I_1&=I_0+x_1-d_1;\\ I_i&=I_{i-1}+x_i-d_i, &&\forall i \in S|i\ge 1; \end{align*} \end{split}\]

Naturaleza de las Variables#

Solo pueden producirse y almacenarse cantidades positivas de cemento:

\[\begin{split} \begin{align*} x_i&\geq 0,&&\forall i \in S;\\ I_i&\geq 0,&&\forall i \in S; \end{align*} \end{split}\]

Función objetivo#

Debe maximizarse la utilidad.

\[ \operatorname{máx}\ \sum_{i\in S}p_{i}d_{i} - c_{i}x_{i} - h_{i}I_{i}. \]

Ya que los ingresos no dependen de las variables de decisión, minimizar los costos es equivalente.

\[ \operatorname{mín}\ \sum_{i\in S}c_{i}x_{i} + h_{i}I_{i}. \]

Implementación#

b. Resuelve el modelo planteado utilizando la librería de PuLP en Python. ¿Cuál es la solución óptima del problema?

Librerías#

Importa el módulo matplotlib.pyplot para crear gráficas y la librería pulp para crear y resolver el modelo.

import matplotlib.pyplot as plt
import pulp as lp

Conjuntos#

Define el conjuntos S que representa las semanas del horizonte de planeación.

Recuerda que por conveniencia de preservar el orden de los elementos de los conjuntos, no siempre deberás definirlos con el tipo set.

# Semanas
S = list(range(1, 13))

Parámetros#

Define o importa los parámetros del modelo.

# Costo de producción por tonelada en la semana i in S
c = {
172.8,
178.7,
174.6,
181.4,
183.0,
177.7,
182.8,
186.8,
181.8,
178.3,
173.4,
168.8,
}

# Costo de almacenamiento por tonelada en la semana i in S
h = {
6.9,
7.2,
8.0,
8.9,
9.0,
7.8,
6.7,
7.3,
7.8,
8.8,
9.2,
8.4,
}

# Demanda de la semana i in S
d = {
95000,
99750,
104738,
109974,
109974,
109974,
120972,
120972,
108875,
97987,
78390,
94068,
}

# Precio por tonelada en la semana i in S
p = {
432.0,
440.6,
449.5,
458.4,
467.6,
477.0,
486.5,
496.2,
506.2,
516.3,
526.6,
537.1,
}

# Inventario inicial de toneladas de cemento
I0 = 12000

Objeto del modelo#

Construye un problema al que luego agregarás las restricciones y la función objetivo.

problema = lp.LpProblem(name="inventarios", sense=lp.LpMaximize)

Variables de decisión#

Define las variables del problema de manera que estén contenidas en diccionarios indexados en los conjuntos de sus variables respectivas.

# Toneladas de cemento a producir en cada semana
x = {
    i: lp.LpVariable(
        name=f"produccion_{i}", lowBound=0, upBound=None, cat=lp.LpContinuous
    )
    for i in S
}

# Toneladas de cemento en inventario al final de cada semana
I = {
    i: lp.LpVariable(
        name=f"inventario_{i}", lowBound=0, upBound=None, cat=lp.LpContinuous
    )
    for i in S
}

Función objetivo#

Agrega al problema la función objetivo. Recuerda que al definir el problema, ya definiste si este es de maximización o minimización.

problema += (
    sum(d[i] * p[i] - x[i] * c[i] - I[i] * h[i] for i in S),
    "utilidad_total",
)

Restricciones#

Agrega al problema las restricciones del modelo.

# Se garantiza que se respeten los limites de producción
for i in S:
    problema += x[i] <= 110000, f"produccion_max_{i}"
    problema += x[i] >= 85000, f"produccin_min_{i}"

# Contabilizar los inventarios de cada semana
problema += I[1] == I0 + x[1] - d[1], "inventario_semana_1"
for i in S:
    if i > 1:
        problema += I[i] == I[i - 1] + x[i] - d[i], f"inventario_semana_{i}"

Resolver el problema#

Invoca el optimizador. Este paso le asigna un valor a las variables incluidas en las restricciones o función objetivo del modelo.

problema.solve()

Welcome to the CBC MILP Solver 
Version: 2.10.8 
Build Date: May  6 2022 

command line - cbc /tmp/74308520c47742ba842d4f714b770609-pulp.mps max timeMode elapsed branch printingOptions all solution /tmp/74308520c47742ba842d4f714b770609-pulp.sol (default strategy 1)
At line 2 NAME          MODEL
At line 3 ROWS
At line 41 COLUMNS
At line 125 RHS
At line 162 BOUNDS
At line 163 ENDATA
Problem MODEL has 36 rows, 24 columns and 59 elements
Coin0008I MODEL read with 0 errors
Option for timeMode changed from cpu to elapsed
Presolve 4 (-32) rows, 16 (-8) columns and 19 (-40) elements
0  Obj -1.8735107e+08 Primal inf 180613.97 (4)
4  Obj -2.2239275e+08
Optimal - objective value -2.2239275e+08
After Postsolve, objective -2.2239275e+08, infeasibilities - dual 0 (0), primal 0 (0)
Optimal objective -222392746.5 - 4 iterations time 0.002, Presolve 0.00
Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.00   (Wallclock seconds):       0.00

Imprimir resultados#

Antes de estudiar el óptimo del modelo, identifica en el estado del optimizador si pudo resolver el problema.

f"Estado del optimizador: {lp.LpStatus[problema.status]}"

'Estado del optimizador: Optimal'

Identifica también el valor de la función objetivo.

f"Utilidad total: {lp.value(problema.objective)}"

'Utilidad total: 380356850.79999995'

Por último, imprime de manera estructurada el valor de las variables de decisión y otras expresiones de interés.

print("Semana", "Producción (ton)", "Inventario (ton)", sep="\t")
for i in S:
    print(i, f"{lp.value(x[i]): .2f}", f"{lp.value(I[i]): .2f}", sep="\t")

Semana	Producción (ton)	Inventario (ton)
89354.00	 6354.00
110000.00	 16604.00
110000.00	 21866.00
110000.00	 21892.00
110000.00	 21918.00
110000.00	 21944.00
110000.00	 10972.00
110000.00	 0.00
108875.00	 0.00
97987.00	 0.00
85000.00	 6610.00
87458.00	 0.00

Visualizar resultados#

Ahora que conoces el valor de las variables de decisión, desarrolla las siguientes visualizaciones del resultado.

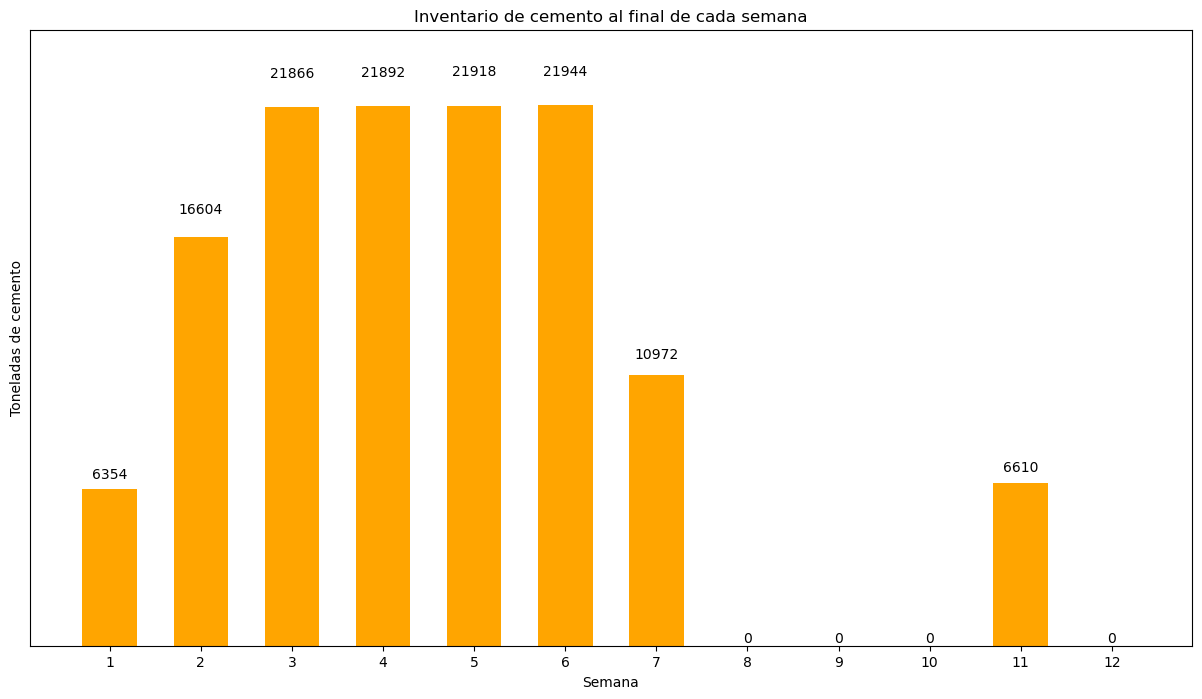
Desarrolla una gráfica que ilustre el nivel de inventario final a lo largo del horizonte de planeación.

# Listas de producción, inventario final e inventario inicial de cada semana
Prod = [lp.value(x[i]) for i in S]
Inv_F = [lp.value(I[i]) for i in S]
Inv_I = [I0] + Inv_F[:-1]

# Gráfica inventario final de cada semana
fig2, ax3 = plt.subplots(figsize=(15, 8))

# Añadir barras a la gráfica
rects2 = ax3.bar(S, Inv_F, width=0.6, tick_label=S, color="orange")

# Etiquetar cada barra con toneladas de cemento en inventario
for rect in rects2:
    height = rect.get_height()
    ax3.text(
        rect.get_x() + rect.get_width() / 2.0,
        1.05 * height,
        "%d" % int(height),
        ha="center",
        va="bottom",
    )

# Título de la gráfica
ax3.set_title("Inventario de cemento al final de cada semana")

# Etiqueta eje x
ax3.set_xlabel("Semana")

# Etiqueta eje y
ax3.set_ylabel("Toneladas de cemento")

# Rango eje y
ax3.set_ylim([0, 25000])

# Remover dígitos del eje y
ax3.set_yticks([])

[]

../../_images/ad365398558482da5caa1738a8eec801533be58cc25120bc102402257595b386.png

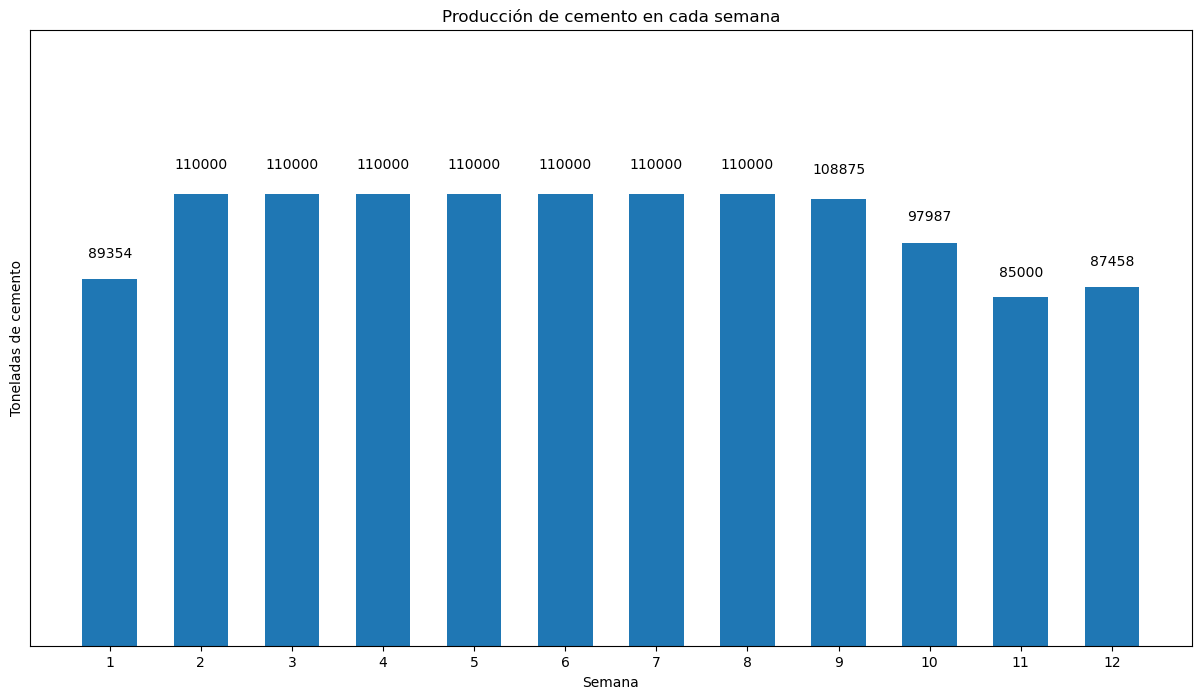
Desarrolla una gráfica que ilustre el nivel de producción a lo largo del horizonte de planeación.

# Gráfica del plan de producción
fig1, ax2 = plt.subplots(figsize=(15, 8))

# Añadir barras a la gráfica
rects1 = ax2.bar(S, Prod, width=0.6, tick_label=S)

# Añadir los labels a cada barra con las toneladas de cemento producidas
for rect in rects1:
    height = rect.get_height()
    ax2.text(
        rect.get_x() + rect.get_width() / 2.0,
        1.05 * height,
        "%d" % int(height),
        ha="center",
        va="bottom",
    )

# Añadir el titulo de la gráfica
ax2.set_title("Producción de cemento en cada semana")

# Etiqueta eje x
ax2.set_xlabel("Semana")

# Etiqueta eje y
ax2.set_ylabel("Toneladas de cemento")

# Rango eje y
ax2.set_ylim([0, 150000])

# Remover dígitos del eje y
ax2.set_yticks([])

[]

../../_images/ca8097f7308873e092dfd4e6055708f3c73be5010720d1740177cd5a136ae7d7.png

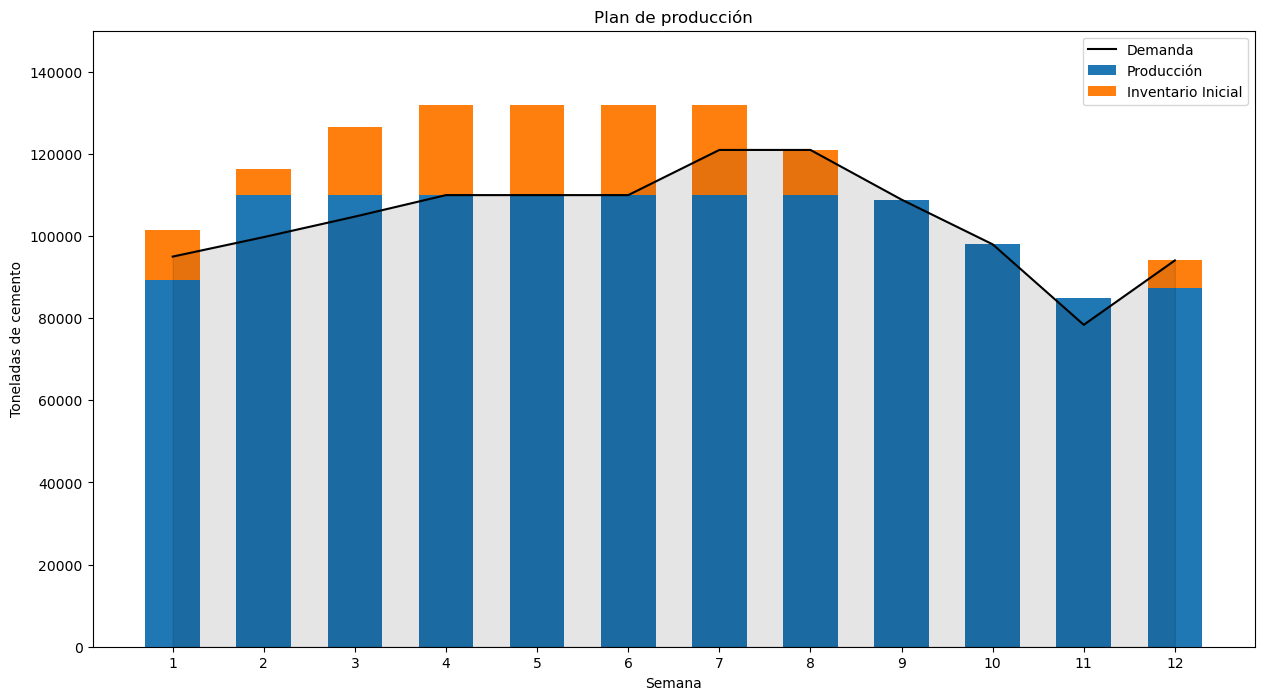
Desarrolla una gráfica que ilustre el nivel de inventario inicial, la producción y la demanda a lo largo del horizonte de planeación.

# Gráfica del plan de producción, demanda e inventario al inicio de cada semana
fig3, ax1 = plt.subplots(figsize=(15, 8))

# Añadir las barras de producción a la gráfica
p1 = ax1.bar(S, Prod, width=0.6, tick_label=S)

# Añadir las barras de inventario inicial a la gráfica
p2 = ax1.bar(S, Inv_I, bottom=Prod, width=0.6, tick_label=S)

# Añadir una línea a la gráfica que represente la demanda
l1 = ax1.plot(S, d.values(), color="black")

# Rellenae el área bajo la curva de demanda
ax1.fill_between(S, d.values(), color="black", alpha=0.1)

# Título de la gráfica
ax1.set_title("Plan de producción")

# Etiqueta eje x
ax1.set_xlabel("Semana")

# Etiqueta eje y
ax1.set_ylabel("Toneladas de cemento")

# Rango eje y
ax1.set_ylim([0, 150000])

# Etiquetas de cada componente de la gráfica
ax1.legend((l1[0], p1[0], p2[0]), ("Demanda", "Producción", "Inventario Inicial"))

<matplotlib.legend.Legend at 0x7ff6489bb350>

../../_images/2181d7bbb34631219d6d103e3bb542809f0711901c682dbeb2a5e374bbbb286b.png

Créditos#

Equipo Principios de Optimización
Autores: Camilo Aguilar, Juan Felipe Rengifo
Desarrollo: Camilo Aguilar, Juan Felipe Rengifo, Alejandro Mantilla
Última fecha de modificación: 07/04/2023

Producción de cemento - Solución

Contents

Producción de cemento - Solución#

Enunciado#

Formulación#

Conjuntos#

Parámetros#

Variables de decisión#

Restricciones#

Naturaleza de las Variables#

Función objetivo#

Implementación#

Librerías#

Conjuntos#

Parámetros#

Objeto del modelo#

Variables de decisión#

Función objetivo#

Restricciones#

Resolver el problema#

Imprimir resultados#

Visualizar resultados#

Créditos#