Transporte de productos lácteos - Solución

Transporte de productos lácteos - Solución#

Tags: Transporte

Enunciado#

La Lechera Ramírez S.A. es una empresa que produce productos lácteos y cuenta con cuatro plantas de producción en Colombia cuyas capacidades de producción mensuales de leche son 1,500, 1,200, 1,400, y 1,000 litros, respectivamente. Estas cuatro plantas suministran leche a los ocho clientes que actualmente tienen, los cuales son distribuidores minoristas de productos. Las demandas mensuales de leche de estos distribuidores son 930, 600, 460, 610, 830, 460, 640 y 240 litros, respectivamente. La Tabla 1 presenta el costo en el que incurre la compañía al enviar un litro de leche desde cada planta hacia cada distribuidor.

Tabla 1. Costos de distribución

	Dist. 1	Dist. 2	Dist. 3	Dist. 4	Dist. 5	Dist. 6	Dist. 7	Dist. 8
Planta 1	650	125	1200	340	150	260	350	800
Planta 2	250	200	250	600	150	950	1050	1000
Planta 3	600	350	400	260	150	300	450	600
Planta 4	450	800	650	250	340	700	600	620

Formula un modelo general de optimización lineal que le permita a La Lechera Ramírez satisfacer la demanda de sus clientes, al menor costo posible.

Formulación#

a. Formula matemáticamente un modelo de optimización de forma general que represente la situación anterior. Defina clara y rigurosamente:

Conjuntos
Parámetros
Variables de decisión
Restricciones
Naturaleza de las variables
Función objetivo

Conjuntos#

\(P\): Plantas
\(D\): Distribuidores

Parámetros#

\(b_i\): oferta de leche de la planta \(i\in P\)
\(t_j\): demanda de leche del distribuidor \(j\in D\)
\(c_{ij}\): costo de envío de un litro de leche de la planta \(i\in P\) al distribuidor \(j\in D\)

Variables de decisión#

\(x_{ij}\): cantidad (en litros) de leche que van de la planta \(i\in P\) al distribuidor \(j\in D\)

Restricciones#

Se debe respetar la oferta disponible de las plantas:

\[ \sum_{j\in D}x_{ij} \le b_i,\ \forall i\in P; \]

Se debe satisfacer la demanda de los distribuidores:

\[ \sum_{i\in P}x_{ij} \ge t_j,\ \forall j\in D; \]

Naturaleza de las Variables#

No pueden enviarse cantidades negativas de leche:

\[ x_{ij} \ge 0,\ \forall i\in P,j\in D; \]

Función objetivo#

Se debe minimizar el costo total:

\[ \operatorname{mín}\ \sum_{i\in P}\sum_{j\in D}x_{ij}c_{ij}. \]

Implementación#

b. Resuelve el modelo planteado utilizando la librería de PuLP en Python. ¿Cuál es la solución óptima del problema?

Librerías#

Importa el módulo matplotlib.pyplot para crear gráficas, la librería networkx para dibujar grafos (redes) y la librería pulp para crear y resolver el modelo.

import matplotlib.pyplot as plt
import networkx as nx
import pulp as lp

Conjuntos#

Define los conjuntos P y D que representan respectivamente las plantas y los distribuidores.

Recuerda que por conveniencia de preservar el orden de los elementos de los conjuntos, no siempre deberás definirlos con el tipo set.

# Plantas
P = ["Planta 1", "Planta 2", "Planta 3", "Planta 4"]

# Distribuidores
D = [
    "Distribuidor 1",
    "Distribuidor 2",
    "Distribuidor 3",
    "Distribuidor 4",
    "Distribuidor 5",
    "Distribuidor 6",
    "Distribuidor 7",
    "Distribuidor 8",
]

Parámetros#

Define o importa los parámetros del modelo.

# Oferta de la planta i en I
b = {
    "Planta 1": 1500,
    "Planta 2": 1200,
    "Planta 3": 1400,
    "Planta 4": 1000,
}

# Demanda del distribuidor j en D
t = {  
    "Distribuidor 1": 930,
    "Distribuidor 2": 600,
    "Distribuidor 3": 460,
    "Distribuidor 4": 610,
    "Distribuidor 5": 830,
    "Distribuidor 6": 460,
    "Distribuidor 7": 640,
    "Distribuidor 8": 240,
}

# Costo de envio de un litro de leche desde la planta i en P al distribuidor j en D.
c = {
    ("Planta 1", "Distribuidor 1"): 650,
    ("Planta 1", "Distribuidor 2"): 125,
    ("Planta 1", "Distribuidor 3"): 1200,
    ("Planta 1", "Distribuidor 4"): 340,
    ("Planta 1", "Distribuidor 5"): 150,
    ("Planta 1", "Distribuidor 6"): 260,
    ("Planta 1", "Distribuidor 7"): 350,
    ("Planta 1", "Distribuidor 8"): 800,
    ("Planta 2", "Distribuidor 1"): 250,
    ("Planta 2", "Distribuidor 2"): 200,
    ("Planta 2", "Distribuidor 3"): 250,
    ("Planta 2", "Distribuidor 4"): 600,
    ("Planta 2", "Distribuidor 5"): 150,
    ("Planta 2", "Distribuidor 6"): 950,
    ("Planta 2", "Distribuidor 7"): 1050,
    ("Planta 2", "Distribuidor 8"): 1000,
    ("Planta 3", "Distribuidor 1"): 600,
    ("Planta 3", "Distribuidor 2"): 350,
    ("Planta 3", "Distribuidor 3"): 400,
    ("Planta 3", "Distribuidor 4"): 260,
    ("Planta 3", "Distribuidor 5"): 150,
    ("Planta 3", "Distribuidor 6"): 300,
    ("Planta 3", "Distribuidor 7"): 450,
    ("Planta 3", "Distribuidor 8"): 600,
    ("Planta 4", "Distribuidor 1"): 450,
    ("Planta 4", "Distribuidor 2"): 800,
    ("Planta 4", "Distribuidor 3"): 650,
    ("Planta 4", "Distribuidor 4"): 250,
    ("Planta 4", "Distribuidor 5"): 340,
    ("Planta 4", "Distribuidor 6"): 700,
    ("Planta 4", "Distribuidor 7"): 600,
    ("Planta 4", "Distribuidor 8"): 620,
}

Objeto del modelo#

Construye un problema al que luego agregarás las restricciones y la función objetivo.

problema = lp.LpProblem(name="Transporte", sense=lp.LpMinimize)

Variables de decisión#

Define las variables del problema de manera que estén contenidas en diccionarios indexados en los conjuntos de sus variables respectivas.

# litros de leche que van de la planta i en P al distribuidor j en D
x = {
    (i, j): lp.LpVariable(
        name=f"litros_planta_{i}_distribuidor_{j}",
        lowBound=0,
        upBound=None,
        cat=lp.LpContinuous,
    )
    for i in P
    for j in D
}

Función objetivo#

Agrega al problema la función objetivo. Recuerda que al definir el problema, ya definiste si este es de maximización o minimización.

problema += sum(c[i, j] * x[i, j] for i in P for j in D), "costos_totales"

Restricciones#

Agrega al problema las restricciones del modelo.

# Se respeta la oferta de cada planta
for i in P:
    problema += (
        sum(x[i, j] for j in D) <= b[i],
        f"oferta_planta_{i}",
    )

# Se satisface la demanda de cada distribuidor
for j in D:
    problema += (
        sum(x[i, j] for i in P) >= t[j],
        f"demanda_distribuidor_{j}",
    )

Resolver el problema#

Invoca el optimizador. Este paso le asigna un valor a las variables incluidas en las restricciones o función objetivo del modelo.

problema.solve()

Welcome to the CBC MILP Solver 
Version: 2.10.8 
Build Date: May  6 2022 

command line - cbc /tmp/592979ddf876456db30dd22b4f5ddd3e-pulp.mps timeMode elapsed branch printingOptions all solution /tmp/592979ddf876456db30dd22b4f5ddd3e-pulp.sol (default strategy 1)
At line 2 NAME          MODEL
At line 3 ROWS
At line 17 COLUMNS
At line 114 RHS
At line 127 BOUNDS
At line 128 ENDATA
Problem MODEL has 12 rows, 32 columns and 64 elements
Coin0008I MODEL read with 0 errors
Option for timeMode changed from cpu to elapsed
Presolve 12 (0) rows, 32 (0) columns and 64 (0) elements
0  Obj 0 Primal inf 4770 (8)
13  Obj 1224800
Optimal - objective value 1224800
Optimal objective 1224800 - 13 iterations time 0.002
Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.00   (Wallclock seconds):       0.00

Imprimir resultados#

Antes de estudiar el óptimo del modelo, identifica en el estado del optimizador si pudo resolver el problema.

f"Estado del optimizador: {lp.LpStatus[problema.status]}"

'Estado del optimizador: Optimal'

Identifica también el valor de la función objetivo.

f"Costo total: {lp.value(problema.objective)}"

'Costo total: 1224800.0'

Por último, imprime de manera estructurada el valor de las variables de decisión y otras expresiones de interés.

for j in D:
    print(f"\t{j}", end="")
print()

for i in P:
    print(i, end="\t")
    for j in D:
        print(lp.value(x[i, j]), end="\t")
    print()

	Distribuidor 1	Distribuidor 2	Distribuidor 3	Distribuidor 4	Distribuidor 5	Distribuidor 6	Distribuidor 7	Distribuidor 8
Planta 1	0.0	600.0	0.0	0.0	0.0	260.0	640.0	0.0	
Planta 2	930.0	0.0	270.0	0.0	0.0	0.0	0.0	0.0	
Planta 3	0.0	0.0	190.0	0.0	830.0	200.0	0.0	180.0	
Planta 4	0.0	0.0	0.0	610.0	0.0	0.0	0.0	60.0	

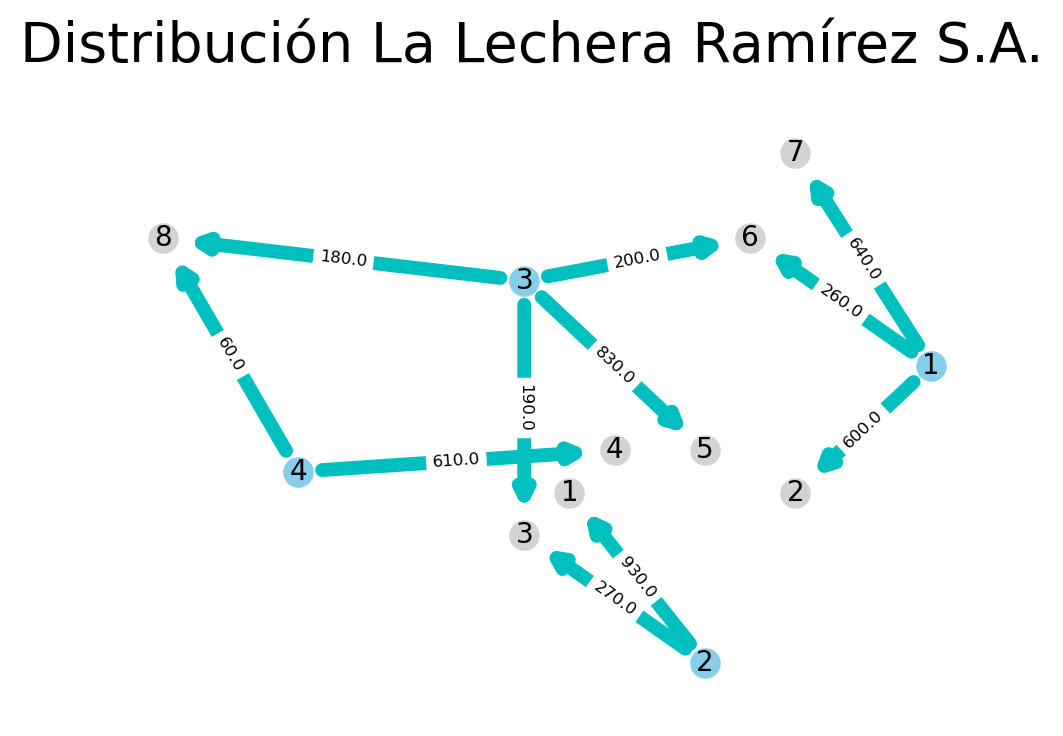
Visualizar resultados#

Ahora que conoces el valor de las variables de decisión, desarrolla una gráfica que ilustre la red de distribución y los envíos dentro de la misma. Utiliza las ubicaciones definidas a continuación.

# Coordenadas de las plantas
coordenadas_plantas = {
    "Planta 1": (9.5, 12),
    "Planta 2": (7, 5),
    "Planta 3": (5, 14),
    "Planta 4": (2.5, 9.5),
}

# Coordenadas de los distribuidores
coordenadas_distribuidores = {
    "Distribuidor 1": (5.5, 9),
    "Distribuidor 2": (8, 9),
    "Distribuidor 3": (5, 8),
    "Distribuidor 4": (6, 10),
    "Distribuidor 5": (7, 10),
    "Distribuidor 6": (7.5, 15),
    "Distribuidor 7": (8, 17),
    "Distribuidor 8": (1, 15),
}

# Se crean dos conjuntos auxiliares para los labels de los nodos de las plantas y distribuidores
labels_plantas = {P[i]: i + 1 for i in range(len(P))}
labels_distribuidores = {D[j]: j + 1 for j in range(len(D))}

# Se crea un conjunto auxiliar para los labels de los arcos
coordenadas = coordenadas_plantas
coordenadas.update(coordenadas_distribuidores)

# Se guarda la solución en un vector
xSol = {(i, j): lp.value(x[i, j]) for i in P for j in D if lp.value(x[i, j]) > 0.01}

# Se modifican las dimensiones de la visualización
plt.rcParams["figure.figsize"] = 6, 4
plt.rcParams["figure.dpi"] = 200

# Creación de un modelo de grafos dirigidos.
G = nx.DiGraph()

# Dibujar los nodos de plantas y distribuidores.
nx.draw_networkx_nodes(
    G, coordenadas_plantas, nodelist=P, node_color="skyblue", node_size=100
)
nx.draw_networkx_nodes(
    G, coordenadas_distribuidores, nodelist=D, node_color="lightgray", node_size=100
)

# Dibujar los labels de los nodos de plantas y distribuidores.
nx.draw_networkx_labels(G, coordenadas_plantas, labels_plantas, font_size=10)
nx.draw_networkx_labels(
    G, coordenadas_distribuidores, labels_distribuidores, font_size=10
)

# Dibujar arcos del diagrama con sus respectivos litros de leche enviados.
nx.draw_networkx_edges(G, coordenadas, xSol, width=5, edge_color="c", arrows=True)
nx.draw_networkx_edge_labels(G, coordenadas, edge_labels=xSol, font_size=6)
nx.draw_networkx(G, coordenadas, with_labels=True)

# Borrar ejes, agregar titulo y mostrar la ventana del diagrama.
plt.axis("off")
nx.draw(G)
plt.suptitle("Distribución La Lechera Ramírez S.A.", fontsize=20)
plt.show()

../../_images/675a0461c8779fc3ce8ffed0e14f61f78e2e82c9fc086820dc36e7982a39822d.png

Créditos#

Equipo Principios de Optimización
Autores: Camilo Aguilar, Juan Felipe Rengifo
Desarrollo: Camilo Aguilar, Juan Felipe Rengifo, Alejandro Mantilla
Última fecha de modificación: 07/04/2023

Transporte de productos lácteos - Solución

Contents

Transporte de productos lácteos - Solución#

Enunciado#

Formulación#

Conjuntos#

Parámetros#

Variables de decisión#

Restricciones#

Naturaleza de las Variables#

Función objetivo#

Implementación#

Librerías#

Conjuntos#

Parámetros#

Objeto del modelo#

Variables de decisión#

Función objetivo#

Restricciones#

Resolver el problema#

Imprimir resultados#

Visualizar resultados#

Créditos#